Ce fil présente les clacul et résultat d'une analyse théorique de ces limites
Contributeurs : nov et Oisan
Retournement
Lors d’un virage serré pris à grande vitesse il arrive un stade où la force centrifuge attein
t une amplitude telle qu’elle dépasse l’effet de la gravité maintenant les trois roues du moskitOS au sol. Le moskitOS bascule alors autour d’un « axe de tonneau » passant par les points d’appui de la roue avant et de la roue arrière située à l’extérieur du virage. Les conséquences plus ou moins dramatiques d’un tel évènement font que sa probabilité d’occurrence doit être limite au maximum. Comme on le verra par la suite, ce résultat est obtenu par un placement du centre de gravité le plus bas et le plus proche de l’essieu arrière possible.
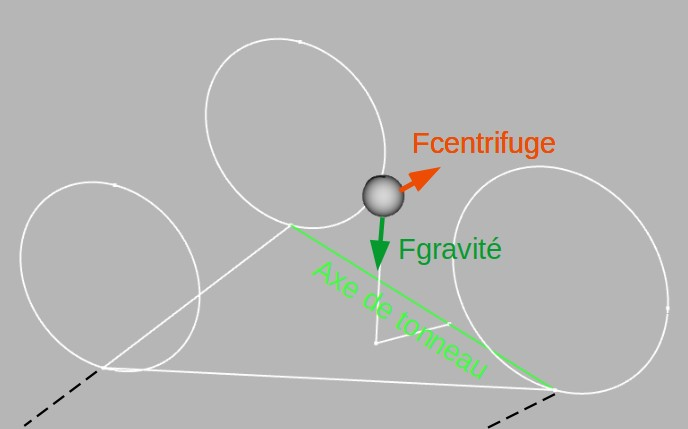
Lors d’un virage serré pris à grande vitesse il arrive un stade le moskitOS bascule alors autour d’un « axe de tonneau » passant par les points d’appui de la roue avant et de la roue arrière extérieure au virage.
Il est important de remarquer que la force centrifuge Fc n’est pas perpendiculaire à l’axe de tonneau. En effet elle est entièrement radiale par rapport à la trajectoire circulaire de centre C (cf. Figure ci-dessous gauche) suivie par le moskitOS en virage. Il faut donc avant tout la projeter perpendiculairement à l’axe de tonneau ce qui est proposé par Fct = Fc*cos(ɵ).
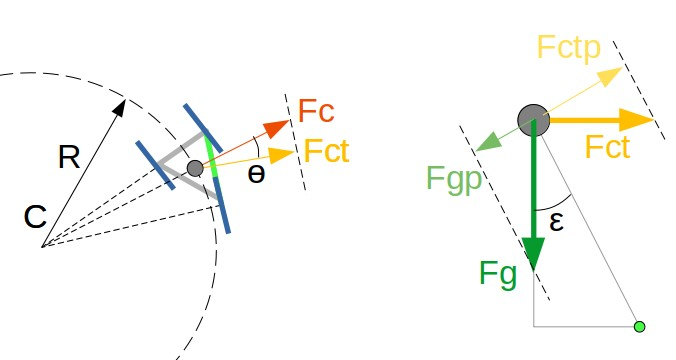
Vue schématique de dessus (gauche) du moskitOS suivant une trajectoire circulaire, et face à l’axe de tonneau (droite).
Une fois toutes les forces dans le plan perpendiculaire à l’axe de tonneau (AdT) passant par le centre de gravité (CdG), il suffit de les projeter perpendiculairement au segment reliant l’AdT au CdG. On a alors :
- Fctp = Fct*cos(ε) (1)
- Fgp = Fg*cos(90-ε) (2)
- Et la condition de non-retournement : Fgp ≥ Fctp (3)
Soit e l’empattement et d la voie du moskitOS, R le rayon la trajectoire circulaire suivie et h la hauteur du centre de gravité par rapport au sol. On suppose que le centre de gravité est situé au milieu de l’empattement, on a :
- ɵ = atan(d/2 / e) – atan(e/2 / R) (4)
- ε = atan(e/2*sin(atan(d/2/e)) / h) (5)
Considérant enfin les forces :
- Fg = m*g, avec m = masse totale MosquitOS + pilote et g = 9,81 m/s2 (6)
- Fc = m*v2 / R, avec v = vitesse du MosquitOS en m/s (7)
Dérapage
Concernant le dérapage il intervient simplement lorsque la force centrifuge Fc excède la force de frottement Ff des pneus sur le sol. On a :
Avec μ le coefficient de frottement soit environ 0,7-0,8 pour une pneu sur route sèche. Considérant (7) ci-dessus la condition d’adhérence devient alors :
- μ*m*g > m*v2 / R → μ*g > v2 / R
Il découle de ci-dessus l’inclinaison maximale du siège, utile afin de compenser la force centrifuge et éviter toute poussée latérale du pilote. Cet angle Δ est celui de la résultante des forces centrifuge Fc et gravitaire Fg. Il est donné par :
- Δ = atan(Fc / Fg) = atan(m*v2 / R / (m*g)) = atan(v2 / (R*g))
Simulation
Une feuille de calcul pré-remplie permettant de tester différents paramètres est disponible ici.
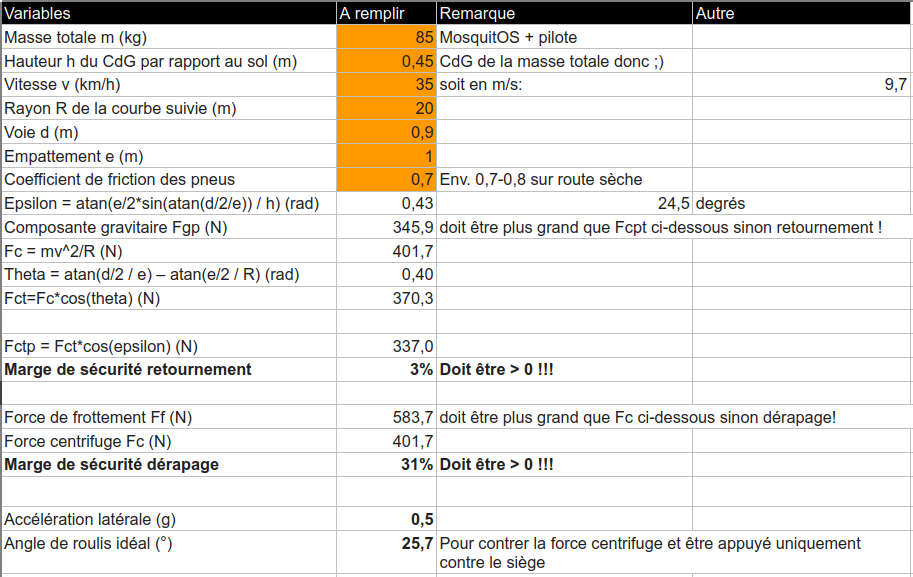
Pour le moskitOS v4 on suppose donc :
pilote 65 kg + moskitOS 20 kg = 85 kg
CdG à 0,45 m du sol
Vitesse de 35 km/h
Virage de 20m de rayon
Voie (distance entre les roues arrières) de 0,9 m
Empattement (distance entre les axes de roue avant et arrière) de 1m
Coefficient de friction des pneus de 0,7 (courant)
Et on trouve :
- Marge au retournement de 3% (limite de se retourner)
- Marge au dérapage de 31% (encore de la marge, le moskitOS se retourne avant de déraper…)
- Accélération latérale de 0,5 G (la moitié de son poids en latéral c'est pas rien, bien sportif le moskitOS)
- Angle de roulis idéal de 26° (à cette vitesse…)
On peut comparer avec d'autres véhicules à 3 roues. Par exemple un vélomobile de 25 + 65 = 90 kg au total avec une voie de 0,7 m ne doit pas dépasser 31 km/h et 0,4 G sur cette même courbe…